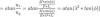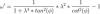AlexisPap

Δεν είμαι σίγουρος αν καταλαβαίνω... αλλά, αν καταλαβαίνω, διαφωνώ: - Στον ασθενή άξονα, εφόσον οι τεγίδες παρεμποδίζουν τον λυγισμό, το L0 είναι η απόσταση μεταξύ των τεγίδων. Η ελαστική γραμμή είναι αμφιαρθρωτής, οπότε Κ=1. - Στον ασθενή άξονα, δεν υπάρχει κάτι που να δεσμεύει τον λυγισμό μεταξύ στύλου και κορφιά. Άρα το L0 είναι η απόσταση στύλου - κορφιά. Το υποστύλωμα παρεμποδίζει σημαντικά την στροφή στον κόμβο στύλου - ζυγώματος, αλλά υπόκειται και αυτό σε αξονικό και είναι επιρρεπές σε λυγισμό. Ομοίως και ο κόμβος του κορφιά... Επομένως είναι αδύνατον να εκτιμήσουμε βάσει διαγράμματος ροπών το Κ. Ξέρουμε ότι είναι μεταξύ 0,5 και 1 αλλά δεν ξέρουμε πόσο είναι. Και λαμβάνουμε 1, που είναι το ασφαλέστερο... Για τους συντελεστές ομοιομορφοποίησης της ροπής, κανονικά κάνεις γραμμική παρεμβολή, μα βάση το πραγματικό διάγραμμα ροπών του ελεγχόμενου μέλους... Jackson, δεν είμαι σίγουρος ότι λέμε το ίδιο πράγμα... εγώ μιλάω για αυτό...

Μιλάς για το ένα δοκάρι του ζυγώματος (το μισό ζύγωμα); Για έλεγχο σε λυγισμό κατά τον ισχυρό άξονα, με ταυτόχρονη ροπή; Η ελαστική του γραμμή είναι κάτι μεταξύ αμφιαρθρωτής και αμφιπάκτου. Δηλαδή το Κ είναι μεταξύ 0,5 και 1. Επειδή δεν μπορείς να ξέρεις πόσο είναι χωρίς την ανάλυση του jackson βάζεις 1 που είναι προς την μεριά της ασφαλείας. Λογικά ο έλεγχος θα βγάλει επάρκεια. Αν τυχόν δεν βγάλει επάρκεια (δεν μου έτυχε ποτέ), μπορείς να πας σε περαιτέρω ανάλυση για να βρεις την πραγματική τιμή του Κ...

ΟΚ, κατάλαβα, ευχαριστώ! Η γραμμική μέθοδος έχει βέβαια κάποιες παραδοχές που μπορεί και να μην είναι πάντα σωστές. Όπως έγραψες, "ακριβής" μέθοδος είναι η μη γραμμική (επαναληπτική)... Νομίζω όμως ότι για τις απλές κατασκευές που συνήθως κάνουμε (χαμηλές κατασκευές, ανοίγματα μέχρι 30m) η χρήση τέτοιων μεθόδων (των γραμμικών και, βεβαίως, των επαναληπτικών) είναι υπερβολή...

Αν θες, πες ποιος είναι αυτός ο έλεγχος, πως δουλεύει...

Όλο το ζύγωμα; Ο έλεγχος λυγισμού (καμπτικού / στρεπτοκαμπτικού) εφαρμόζεται σε γραμμικά μέλη, όχι σε μορφώματα... Πως θα εφαρμοστεί σε όλο το ζύγωμα; Ανάλυση λυγισμού, εννοείς P/Δ; Είναι πολύ απίθανο το ζύγωμα να έχει πρόβλημα λυγισμού στον ισχυρό άξονα. Συνήθως το μόνο πρόβλημα που αντιμετωπίζουμε είναι ο στρεπτοκαμπτικός...

Ε, καλά, μην πνιγόμαστε σε μια κουταλιά νερό... Ποιος σε υποχρεώνει να κάνεις δοκάρι πάνω από το παράθυρο;

Στα ζευκτά έχουμε δύο πέλματα τα οποία έχουν ισχυρό και ασθενή άξονα και ελέγχονται σε καμπτικό λυγισμό (πολύ σπάνια και σε στρεπτοκαμπτικό)... Αλλά από το σχήμα είναι φανερό ότι αναφέρεσαι σε πλαίσιο του οποίου το ζύγωμα υποφέρει μόνο σε στρεπτοκαμπτικό ("πλευρικό" σύμφωνα με την ορολογία της τριανδρίας)... Όχι... Γενικά το μήκος λυγισμού δεν το επιλέγουμε βάσει διαγράμματος ροπών. Ξεκινάμε από το βασικό μήκος που είναι το μήκος μεταξύ δύο διαδοχικών δεσμεύσεων της πλευρικής παραμόρφωσης. Ανάλογα με τις συνθήκες πλευρικής εξασφάλισης προκύπτει η λυγηρότητα. Ανάλογα με το διάγραμμα των ροπών προκύπτουν οι διορθωτικοί συντελεστές ομοιόμορφης ροπής. Από 'κει και πέρα, κάθε κατασκευή (τεγίδες, επικαλύψεις, ντίζες, σύνδεσμοι κλπ) που συνδέει επαρκώς το θλιβόμενο πέλμα με κάποιο σύστημα δυσκαψίας στην διεύθυνση του λυγισμού αποτελεί πλευρική εξασφάλιση και περιορίζει το μήκος λυγισμού.

Ω, όχι, όχι!!! :) τουλάχιστον όχι ...για αρκετό καιρό... :)

Γιάννη.... αφού τα είπαμε! τα βρασμένα ζυμαρικά δεν υπακούουν στον νόμο του Hook! Μόνο εργαστηριακά μπορείς να τα μελετήσεις: :):):) CostasV, για να βγάλεις άκρη με τον Euler πρέπει να λύσεις τις εξισώσεις του για το φουσίλι... μάλλον δύσκολο! Όσο για την ελάχιστη ροπή αδρανείας, νομίζω ότι δεν υπάρχει ελάχιστος περιορισμός: όσο το βήμα μικραίνει, πέφτει και η δυσκαμψία...

Το έκαναν για να μην γίνονται υπόγεια με "άτυπη" κύρια χρήση. Δοθέντος ότι οι φεγγίτες 80cm εξασφαλίζουν καλό φωτισμό και ότι με λίγη επιμονή στον σχεδιασμό μπορείς (κάνοντας χρήση της τοπικής εκσκαφής) να βγάλεις ισόγεια είσοδο και κανονικά παράθυρα, έχω δει υπόγεια σύννομα με εξαιρετικές προϋποθέσεις κύριας χρήσης... Τελικά η επιλογή της μείωσης στα 80cm ήταν άλλη μια ανοησία. Ο ασυδότως παρανομών δεν κολλάει σε τέτοια, ξεμπαζώνει (δηλ... αλλάζει στάθμη) και καθαρίζει...

Λοιπόν, μάλλον δεν θα έχουμε μαθηματική απόδειξη... Είναι προφανές ότι η αρχή Bernoulli δεν ισχύει. Μπορούμε σχετικά εύκολα να δείξουμε ότι η διατομή στρεβλώνεται. Επίσης, μπορούμε με την ίδια μέθοδο που αποδεικνύουμε την ισχύ της αρχής Bernoulli, να δείξουμε ότι η παραμόρφωση της διατομής είναι καθαρή γραμμική στρέβλωση (κατά τον "μεγάλο" άξονα της διατομής). Το πρόβλημα είναι ότι δεν έχουμε επίπεδη ένταση και η γεωμετρία του φορέα μας είναι πολύπλοκη. Που σημαίνει ότι το πρόβλημα δεν φαίνεται να έχει αναλυτική λύση. Επομένως περιοριζόμαστε σε φουσίλι με μεγάλο βήμα για το οποίο είναι επαρκής η τεχνική θεωρία της κάμψης... Τα φουσίλι μικρού βήματος μόνο με πεπερασμένα! Για όποιον θέλει να κάνει ανασκόπηση της θεωρίας της ελαστικότητας και των μαθηματικών που την συνοδεύουν, καθώς και να δει πως εφαρμόζεται σε συμμετρικές πρισματικές δοκούς (θεωρώντας επίπεδη ένταση και αξιοποιώντας την αρχή Saint-Venant) προτείνω πρώτο τόμο Τσαμασφύρου...

Σαφώς υπάρχουν ΔΕΠ που χρησιμοποιούν πανεπιστημιακό εξοπλισμό και φοιτητικό δυναμικό νομίμως, για "ερευνητικά προγράμματα". Αλλά αυτά τα κάνουν οι ψιλικατζήδες. Το μεγάλο εμπορεύσιμο ατού είναι ο τίτλος... Όποιοι πιάσαν το νόημα ανοίξαν εταιρίες...

Εκτός σχεδίου 0,80m Εντός σχεδίου 1,50m από στάθμη διαμορφωμένου εδάφους μέχρις στάθμης οροφής υπογείου. Δεν είναι θέμα γνώμης της Πολεοδομίας, απλώς έτσι είναι.

Κατάλαβες καλά. Δοθέντος ότι τα υγρά είναι ασυμπίεστα και η παραμορφωσιμότητα των σωλήνων (ειδικά αν είναι σιδηρές) περιορισμένη, δεν θα χρειαστεί να περιμένεις τόσο πολύ. Μέσα σε λίγα λεπτά και η μικρότερη διαρροή θα γίνει αντιληπτή... Με του Erling κράτα μια μικρή επιφύλαξη: Η μέθοδος δουλεύει άριστα όταν έχεις βόθρο, που σημαίνει ότι έχεις μία συγκεντρωμένη ποσότητα νερού στην οποία προσθέτεις χρωστική και περιμένεις. Στην αποχέτευση δεν ξέρεις τι ποσοστό της παροχής καταλήγει σε διαρροή. Δεν μπορείς να τροφοδοτείς την αποχέτευση συνέχεια (επί ώρες ή μέρες) περιμένοντας πότε θα λάβεις ένδειξη. Δεν ξέρεις αν η διαρροή συμβαίνει με χαμηλή ροή ή με υψηλή ροή... Που σημαίνει ότι μπορεί να ρίξεις το υλικό με έναν τρόπο που να τον θεωρείς σωστό, να μην λάβεις ένδειξη, αλλά παρόλα αυτά διαρροή να υπάρχει...

Ο σχηματισμός των νεφών μπορεί να συμβεί οπουδήποτε, αρκεί να πέσει η θερμοκρασία της αντίστοιχης αέριας μάζας... Σαν να μου φαίνεται ότι οι φωτογραφίες τραβήχτηκαν απόγευμα!

Αν R η ακτίνα καμπυλότητας, το u=1/R είναι η καμπυλότητα. Έχει τιμή Μ/ΕJ. Μια που είναι η ροπή δια έναν πραγματικό αριθμό την απεικονίζω όπως και την ροπή, με διπλό βέλος, κάθετα στο διάνυσμα του βέλους κάμψης. Μια που μας αρέσουν τα μαθηματικά, ας δούμε το θέμα από αναλυτικής απόψεως: Η διατομή έχει πλάτος b και ύψος h = λ*b. Η γωνία που σχηματίζει η ροπή με τον άξονα ψ είναι "φ". Οι ροπές αδρανείας είναι: Iz = hb³/12 = λb^4/12 και Iy = bh³/12 = λ³b^4/12 = λ²*Iz οι συνιστώσες καμπυλότητες στους κύριους άξονες είναι: uyy = Myy/(E*Iy) = M*cos(φ)/(E*Iy) και uzz = Mzz/(E*Iz) = M*sin(φ)/(λ²*Ε*Ιy) Η γωνία θ που σχηματίζει η καμπυλότητα με τον άξονα ψ είναι: Η γωνία ω που σχηματίζει το διάνυσμα της καμπυλότητας με το διάνυσμα της ροπής είναι: Της συνάρτησης αυτής "ω(φ)" είναι το πρώτο από τα διαγράμματα που είχα βάλει στο #17. Όπως φαίνεται η μορφή της συνάρτησης εξαρτάται αποκλειστικά από τον λόγο των πλευρών της διατομής... Πότε έχουμε μέγιστο; θα χρειαστεί να παραγωγίσουμε ως προς φ... και να εξισώσουμε με το 0: Ωραία εξίσωση, αλλά δεν ξέρω πως λύνεται, αν λύνεται... Γι αυτό και στο προηγούμενο ερώτημά σου απάντησα αόριστα "γύρω στις 22°". Όποιος ξέρει την λύση ας βοηθήσει... Υ.Γ1: λόγω βιασύνης, μπορεί να έκανα κάποιο λάθος στην παραγοντοποίηση της τελευταίας (και μόνης) εξίσωσης. Αν κάποιος ασχοληθεί, ας προσέξει. Edit: μόλις είδα ότι ο τελευταίος παράγοντας της εξίσωσης έπρεπε να έχει αρνητικό πρόσημο... Προσοχή! Υ.Γ2: Κώστα, προφανώς γράφαμε μαζί... αλλά σε άλλες κατευθύνσεις. Αν δεν σε κάλυψα επανάλαβε... Υ.Γ3: Και μην ξανακούσω σχόλια, ότι το επίπεδο στην "κουβέντα" είναι χαμηλό! :)

Εξαιρετικό λίνκ Κώστα! Συγχαρητήρια!

Το ρολόι σταματάει να μετράει όταν από την βρύση τρέχει μια κλωστούλα νερό (που γίνεται σταγόνες σε απόσταση ~15cm). Αυτό που είπα είναι να βάλεις κάπου ένα μανόμετρο (εύκολο σε έναν εξωτερικό κρουνό που έχει σπείρωμα 1/3'', να κλείσεις την βάνα στο ρολόι και να δεις αν διατηρείται η πίεση.

Φίλε nikosk64, αναφέρεσαι σε μία -δυστυχώς- όχι σπάνια (για την προσωπική μου εμπειρία) περίπτωση. Είναι δύσκολο να σχολιάσω, καθώς το τίμημα που έχει να πληρώσει ο κύριος του έργου για ένα "λάθος" κατά την κατασκευή του έργου του είναι επαχθέστατο... Μπορώ μόνο να τονίσω για μια ακόμη φορά ότι είναι απολύτως αναγκαία η καλή και στενή συνεργασία του μηχανικού με τον κύριο του έργου, τον εργολάβο, τα συνεργεία. Αν δεν υπάρχει κλίμα συνεργασίας (συμβαίνει, άνθρωποι είμαστε) είναι καλύτερο να σταματάει και η επαγγελματική σχέση. Μηχανικοί, (όπως και πελάτες) υπάρχουν πολλοί... Καταλαβαίνεις βέβαια, δεν μπορώ να υπεισέλθω σε θέματα ευθυνών. Συμμετέχω στο φόρουμ "ανώνυμα" θα ήταν ανεύθυνο να αρχίσω να λέω εύκολες "εξυπνάδες"...

Για να βεβαιωθείς ότι στο Α δεν υπάρχει διαρροή στην ύδρευση (κρύο - ζεστό - θέρμανση): Μόνο με παρακολούθηση της πίεσης, έχοντας κλείσει το ρολόι. Το ρολόι από μία παροχή και κάτω δεν γράφει... (άντε, μην σας βάζω παράξενες ιδέες! ) Για να βεβαιωθείς ότι η αποχέτευση δεν έχει διαρροή: Πολύ δύσκολο, ίσως ανιχνεύοντας το νερό για ουρία ή ενώσεις του αζώτου γενικώς. Αλλά αν βρεις ουρία, πως ξέρεις ότι είναι του γείτονα; Το κακό είναι ότι τα περισσότερα εδάφη φιλτράρουν αποτελεσματικότατα τα αιωρούμενα σωματίδια... Το νερό πάντα βγαίνει σχεδόν άοσμο και διαυγές. Η ύπαρξη τασιενεργών δεν σημαίνει κατ' ανάγκη απορρυπαντικό, μπορεί να προέρχονται και από την άργιλο... Μία λύση είναι ενδεχομένως να φράξεις με μπαλόνι την έξοδο στο κεντρικό φρεάτιο, να γεμίσεις την αποχέτευση με νερό, και να δεις αν μπορεί να το κρατήσει... Όμως αν δεν το κρατάει, δεν σημαίνει ότι έχει σώνει και καλά διαρροή υπό κανονικές συνθήκες λειτουργίας. Ίσως μπορείς να κάνεις ενδοσκόπηση με τις κάμερες που έχουν οι αποφράκτες. Αν οι κλίσεις είναι σωστές, οι μούφες έχουν την σωστή φορά και οι σωλήνες δεν είναι σπασμένες, δεν υπάρχει διαρροή... Ωστόσο δεν είναι καθόλου σίγουρο ότι μπορείς να κάνεις κάτι απ' όλα αυτά...

Μόλις την κατέβασα από την μηχανή. Τραβηγμένη απ' το νησάκι, μέρα - μεσημέρι... Να και ένα γενικό πλάνο:

Για την πληρότητα του θέματος: Ιωάννινα, 08/09/2010, απολύτως ανέφελη μέρα, ακριβώς πάνω από την πόλη: αυτό δεν είναι chemtrail; :)

Γύρω στις 22°. Φυσικά αυτό το διάγραμμα είναι για συγκεκριμένη διατομή με λόγο πλευράς 1:3. Δεν ισχύει για άλλες δοκούς. Ναι, το διάγραμμα το έφτιαξα να έχει τιμές γωνίας στον άξονα χ... Αλλά, εφόσον το βήμα είναι σταθερό, η αναλογία Δφ/Δl είναι σταθερή και θα μπορούσε ο άξονας χ να εχει τιμές μήκους... Edit: Να ένα ακόμη λάθος! το διάγραμμα δεν ήταν b/h = 1:3, αλλά 1:2,5...

Επαναλαμβάνομαι, αλλά με βάση τα νέα δεδομένα οφείλω να ξανά - τοποθετηθώ: Ανάξιο λόγου.Το φορτίο των βιβλιοθηκών δεν πρέπει να λογιστεί στην φορτιζόμενη επιφάνεια αλλά στην επιφάνεια της πλάκας.

Δεν είναι ασυμμετρία. Παρουσιάζω το διάγραμμα από 0 μέχρι π/2 (90°). Από π/2 μέχρι π το διάγραμμα θα είναι συμμετρικό αυτού που παρουσίασα. Στις επόμενες περιόδους απλώς επαναλαμβάνονται. Σε κάθε δοκό σταθερής διατομής η ελαστική γραμμή είναι επίπεδη. Το επίπεδό της είναι κάθετο στην ροπή, εφόσον η ροπή είναι κάθετη / παράλληλη με τους κύριους άξονες της διατομής.