-
Περιεχόμενα
23 -
Εντάχθηκε
-
Τελευταία επίσκεψη
Τύπος περιεχομένου
Profiles
Φόρουμ
Downloads
Gallery
Ειδήσεις
Media Demo
Αγγελίες
Store
Everything posted by gioko
-

Υπολογισμός ενεργειακού κόστους θέρμανσης
file σχολίασε στο gioko's thermoidravliki@ στις 5.1 Λογισμικό
-
-

Υπολογισμός απόδοσης ισχύς σωμάτων τύπου Panel - Φέτες
file σχολίασε στο gioko's thermoidravliki@ στις 5.1 Λογισμικό
-
-
-
-
-
-

Αγγλικό Εικονογραφημένο Λεξικό Τεχνικών Όρων
file σχολίασε στο gioko's georgegaleos στις 14. Διάφορα
-

Ετήσια απόδοση συστημάτων θέρμανσης με Λέβητες και Αντλίες Θερμότητας
file σχολίασε στο gioko's Engineer στις 5.4 Μελέτες-Βοηθήματα
-

Υπολογισμός απόδοσης ισχύς σωμάτων τύπου Panel - Φέτες
file σχολίασε στο gioko's thermoidravliki@ στις 5.1 Λογισμικό
-

Υπολογισμός απόδοσης ισχύς σωμάτων τύπου Panel - Φέτες
file σχολίασε στο gioko's thermoidravliki@ στις 5.1 Λογισμικό
-

Υπολογισμός Κατανάλωσης Καυσίμου (Αυτοκίνητα)
file σχολίασε στο gioko's Samdreamth στις 5.1 Λογισμικό
-
-
-
-

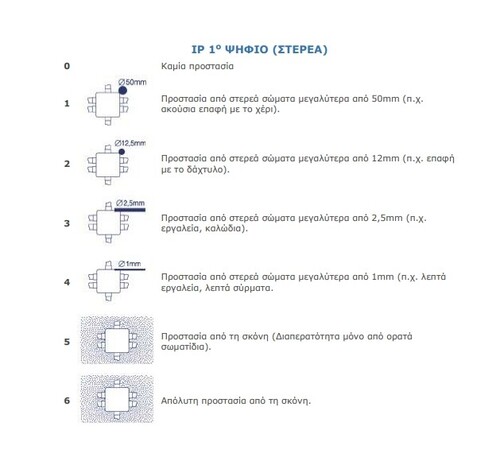
Πίνακας επεξήγησης των δεικτών του βαθμού προστασίας IP
file σχολίασε στο gioko's Marios Kar στις 6.4 Μελέτες-Βοηθήματα
-

Επιμετρήσεις σωλήνων, αεραγωγών και καλωδίων AutoCAD add-in
file σχολίασε στο gioko's Samdreamth στις 5.1 Λογισμικό
-

Συγκριτική Μελέτη απόδοσης Συστημάτων Θέρμανσης
file σχολίασε στο gioko's mechpanos στις 5. Μηχανολογικά
-

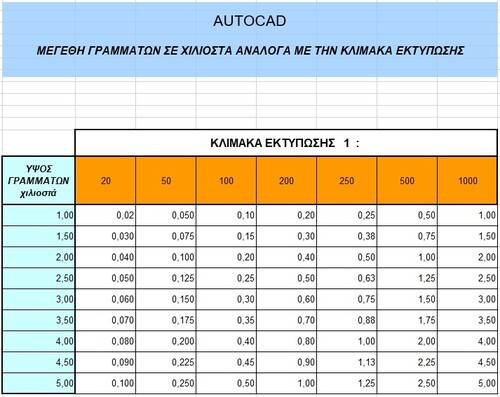
Μέγεθος γραμμάτων ανάλογα με την κλίμακα εκτύπωσης
file σχολίασε στο gioko's Engineer στις 3.4 Μελέτες-Βοηθήματα
- 15 σχόλια
-
- γραμματοσειρά
- autocad
-
(and 2 more)
Με ετικέτα:
-

Υπομνήματα για σχέδια Autocad σε 1:50 και 1:100
file σχολίασε στο gioko's gvarth στις 5.4 Μελέτες-Βοηθήματα
-

Υπολογισμός κατανάλωσης πετρελαίου με ωρομετρητές
gioko replied to sebastian leto's θέμα in Ενεργειακά
ΚΟΙΤΑΞΤΕ ΑΥΤΕΣ ΤΙΣ ΑΝΑΛΥΤΙΚΕΣ ΟΔΗΓΙΕΣ ΚΑΙ ΤΑ ΠΑΡΑΔΕΙΓΜΑΤΑ, ΘΑ ΣΑΣ ΛΥΣΕΙ ΟΛΕΣ ΤΙΣ ΑΠΟΡΙΕΣ... ΚΑΛΗ ΜΕΛΕΤΗ. Κατανομή κοινοχρήστων στην Κεντρική Θέρμανση Σύστημα αυτονομίας με ωρομετρητές Για να υπολογίσουμε το ποσοστό συμμετοχής (στο πετρέλαιο) κάθε διαμερίσματος εφαρμόζουμε την εξίσωση δαπανών που είναι η ακόλουθη: Π (%) = [fi x εi + (1 - Σ(fi x εi) x (εi x ωi)/(Σ (εi x ωi))] x 100. Όπου: Π (%) είναι το ποσοστό συμμετοχής του διαμερίσματος στις δαπάνες θέρμανσης (ΜΟΝΟ πετρέλαιο). Τα fi και εi είναι σταθεροί συντελεστές που βρίσκονται στον πίνακα κατανομής δαπανών που συνέταξε ο μηχανικός για την οικοδομή. Είναι συντελεστές που υπολογίζονται μαθηματικά και πρακτικά δεν σημαίνουν τίποτε. Είναι δηλαδή ενδιάμεσα στάδια του υπολογισμού, χωρίς να σημαίνουν κάτι από μόνοι τους. ωi είναι η ένδειξη του ωρομετρητή (σε ώρες) για το διαμέρισμα i. Το fi λέγεται συντελεστής παραμένουσας επιβάρυνσης ιδιοκτησίας και βγαίνει από την πράξη: fi = ω - ( x + y + z ) Όπου: ΣΥΝΤΕΛΕΣΤΗΣ ω 1) Για κτήρια με θερμομόνωση σύμφωνα με τον κανονισμό ω=0.55 για ρετιρέ και διαμερίσματα πάνω από πιλοτές ω=0.60 για τα υπόγεια και ημιυπόγεια ω=0.65 για ενδιάμεσα διαμερίσματα 2) Για κτίρια χωρίς θερμομόνωση σύμφωνα με τον κανονισμό ω=ο.45 για ρετιρέ και διαμερίσματα πάνω από πιλοτές ω=0.50 για διαμερίσματα σε υπόγειο και ημιυπόγειο ω=0.55 για ενδιάμεσα διαμερίσματα ΣΥΝΤΕΛΕΣΤΗΣ x 1) χ=0 αν οι κεντρικές σωληνώσεις για περισσότερα από τα 2/3 των σωμάτων της ιδιοκτησίας διέρχονται μέσα από την ιδιοκτησία. 2) x=0.06 αν οι κεντρικές σωληνώσεις λιγότερο από το 1/3 των σωμάτων διέρχονται μέσα από την ιδιοκτησία, ή αν οι κεντρικές σωληνώσεις θέρμανσης διέρχονται από κοινόχρηστους χώρους (πλειοψηφία των οικοδομών με σύγχρονη κατασκευή) 3) x=0.03 για τις υπόλοιπες περιπτώσεις. ΣΥΝΤΕΛΕΣΤΗΣ y Το y εξαρτάται από το εμβαδόν του διαμερίσματος και είναι: y=0 για εμβαδόν ίσο ή μεγαλύτερο από 110m2 y=0.04 για εμβαδόν από 75m2 μέχρι 109.99m2 y=0.08 για εμβαδόν από 40m2 μέχρι 74.99m2 y=0.12 για εμβαδόν μικρότερο από 40m2 ΣΥΝΤΕΛΕΣΤΗΣ z Το z εξαρτάται από τον παράγοντα σf= Fεξi / Fπαρi όπου : Fεξi = ΕΞΩΤΕΡΙΚΗ παράπλευρη επιφάνεια της ιδιοκτησίας ΧΩΡΙΣ την οροφή και το δάπεδο. Fπαρi = ΣΥΝΟΛΙΚΗ παράπλευρη επιφάνεια της ιδιοκτησίας ΧΩΡΙΣ την οροφή και το δάπεδο. Αν σf <= 0.20 τότε z = 0.00 0.20 < σf <= 0.35 τότε z = 0.05 0.35 < σf <= 0.50 τότε z = 0.10 0.50 < σf <= 0.65 τότε z = 0.15 σf > 0.65 τότε z = 0.20 ΠΑΡΑΔΕΙΓΜΑ 1ο (εύρεση fi) Έστω λοιπόν ότι έχουμε μία οικοδομή κάτοψης 10x12m (εμβαδόν κάτοψης 120m2) με τέσσερα διαμερίσματα. Η οικοδομή έχει θερμομονωθεί σύμφωνα με τον κανονισμό θερμομόνωσης (πάντα το υποθέτουμε σε καινούριες οικοδομές) και ότι οι κεντρικές σωληνώσεις διέρχονται από τον διάδρομο της οικοδομής. Η οικοδομή του παραδείγματός μας έστω ότι έχει: Ένα διαμέρισμα στο ισόγειο (Δ1)(όχι πυλωτής) (120m2, συνολική παράπλευρη επιφάνεια = (10 + 12 + 10 + 12) x (ύψος = π.χ. 3m) = 132m2 και έστω ότι τα 100m2 είναι εξωτερική επιφάνεια, δηλαδή μόνο τα 32m2 παράπλευρης επιφάνειας χωρίζουν την ιδιοκτησία από εσωτερικό χώρο) Δύο διαμερίσματα στον 1ο (Δ2)και (Δ3)(60 + 60 m2 με έστω 80m2 συνολική παράπλευρη επιφάνεια το καθένα και 45m2 εξωτερική παράπλευρη επιφάνεια) και Ένα διαμέρισμα στον δεύτερο (Δ4)(120m2 με συνολική παράπλευρη 132m2 και εξωτερική παράπλευρη 100m2) (τα εμβαδά είναι μικτά) τότε θα έχουμε τους ακόλουθους συντελεστές: διαμέρισμα Δ1: ω = 0.60 x = 0.06 y = 0 σf = 100/132 = 0.7575 --> z = 0.20 και συνεπώς fi = ω - ( x + y + z ) = 0.60 - ( 0.06 + 0 + 0.20) = 0.34 διαμέρισμα Δ2: ω = 0.65 x = 0.06 y = 0.08 σf = 45/80 = 0.5625 --> z = 0.15 και συνεπώς fi = ω - ( x + y + z ) = 0.65 - ( 0.06 + 0.08 + 0.15) = 0.36 διαμέρισμα Δ3: ω = 0.65 x = 0.06 y = 0.08 σf = 45/80 = 0.5625 --> z = 0.15 και συνεπώς fi = ω - ( x + y + z ) = 0.65 - ( 0.06 + 0.08 + 0.15) = 0.36 διαμέρισμα Δ4: ω = 0.55 x = 0.06 y = 0.0 σf = 100/132 = 0.7575 --> z = 0.20 και συνεπώς fi = ω - ( x + y + z ) = 0.55 - ( 0.06 + 0 + 0.20) = 0.29 Ο εi λέγεται συντελεστής επιβάρυνσης ιδιοκτησίας, και υπολογίζεται από την εξίσωση: εi = Qi / ΣQi Όπου Qi οι απώλειες του διαμερίσματος i και ΣQi οι συνολικές απώλειες της οικοδομής. (το Σ στα μαθηματικά σημαίνει σύνολο - άθροισμα). ΠΑΡΑΔΕΙΓΜΑ 2ο (εύρεση εi) Στα παραπάνω τέσσερα διαμερίσματα αν π.χ. έχουμε απώλειες Δ1=18.000 kcal/h, Δ2=9.000 kcal/h, Δ3=9.000 kcal/h, Δ4=22.000 kcal/h τότε το ΣQi είναι 58.000 kcal/h και τα εi θα είναι Δ1=0.3103, Δ2=0.1552, Δ3=0.1552 και Δ4=0.3793 (θα πρέπει πάντα να στρογγυλεύονται τα νούμερα στο τελευταίο δεκαδικό ώστε να δίνουν άθροισμα ΑΚΡΙΒΩΣ 1.0000) Έχουμε λοιπόν ανακεφαλαιώνοντας τα παρακάτω μεγέθη για κάθε Διαμέρισμα Δ1 fi=0.34 εi=0.3103 ωi=10(π.χ) fi x εi=0.1055 εi x ωi=3.103 Δ2 fi=0.36 εi=0.1552 ωi=10(π.χ) fi x εi=0.0559 εi x ωi=1.552 Δ3 fi=0.36 εi=0.1552 ωi=10(π.χ) fi x εi=0.0559 εi x ωi=1.552 Δ4 fi=0.29 εi=0.3793 ωi=10(π.χ) fi x εi=0.11 εi x ωi=3.793 Το άθροισμα των fi x εi των τεσσάρων διαμερισμάτων είναι 0,3273 και επομένως: (1 - Σ(fi x εi)=1-0,3273=0.6727 (Σ (εi x ωi)=3.103+1.552+1.552+3.793=10 ΠΑΡΑΔΕΙΓΜΑ 3ο (εφαρμογή του τύπου) Εφαρμόζοντας τον τύπο βρίσκουμε: Ποσοστό συμμετοχής για Δ1 Π (%) = [fi x εi + (1 - Σ(fi x εi) x (εi x ωi)/(Σ (εi x ωi))] x 100. Π (%) = [0.1055+(0.6727 x 3.103/10)] x 100 Π (%) =(0.1055+0.2087) x 100 Π (%) =31,42 Ποσοστό συμμετοχής για Δ2 και Δ3 Π (%) =[0.0559+(0.6727 x 1.552/10)] x 100 Π (%) =(0.0559+0.1044) x 100 Π (%) =16.03 Ποσοστό συμμετοχής για Δ4 Π (%) =[0.11+(0.6727 x 3.793/10)] x 100 Π (%) =(0.11+0.2552) x 100 Π (%) =36.52 Συμπεράσματα- Παρατηρήσεις Στην πρώτη εξίσωση ( Π (%) = [fi x εi + (1 - Σ(fi x εi) x (εi x ωi)/(Σ (εi x ωi))] x 100) υπάρχει ένα μέρος σταθερό ανεξάρτητο από την ένδειξη των ωρομετρητών. Είναι το 1ο τμήμα της εξίσωσης fi x εi. Το τμήμα αυτό εξαρτάται από τα γεωμετρικά χαρακτηριστικά του διαμερίσματος (εμβαδόν, παράπλευρες επιφάνειες, απώλειες κ.λ.π.). Εκτός του σταθερού, υπάρχει και το 2ο τμήμα της εξίσωσης, το κλάσμα (εi x ωι)/Σ(εi x ωi) το οποίο λαμβάνει υπ' όψη τις ενδείξεις των ωρομετρητών. Στον υπολογισμό των ποσοστών συμμετοχής (στο πετρέλαιο) λοιπόν συμμετέχει και το σταθερό και το μεταβλητό μέρος. Δεν ισχύει το ίδιο για τα έκτακτα έξοδα (δαπάνες συντήρησης κ.λ.π.) τα οποία υπολογίζονται βάσει ΜΟΝΟ του σταθερού μέρους fi x εi . Αυτό που θα πρέπει να προσέξει κανείς, είναι ότι τα Qi κ.λ.π. είναι οι ΑΠΩΛΕΙΕΣ στα διαμερίσματα και ΟΧΙ τα εγκατεστημένα σώματα. Είναι άδικο να μπαίνουν στον πίνακα σαν παράμετροι οι απώλειες του κτιρίου και όχι τα εγκατεστημένα σώματα, πράγμα που σημαίνει πρακτικά ότι όποιος βάλει μεγαλύτερα σώματα στο σπίτι του "κλέβει" τους άλλους νόμιμα, αλλά δυστυχώς αυτός είναι ο νόμος και έτσι είναι νόμιμος ο υπολογισμός κατανομής δαπανών. Κάποιοι υπολογίζουν τον πίνακα με εγκατεστημένα σώματα, αλλά μπορεί κάποιος ιδιοκτήτης να προσβάλει τον πίνακα αυτόν, με συνέπεια μπερδέματα μεταξύ των ενοίκων και σκοτούρες για τον μηχανικό. Επίσης, το ποσοστό 30% (πάγιο) είναι επίσης λανθασμένο. Το ποσοστό αυτό διαφέρει από οικοδομή σε οικοδομή και ισούται με Σ(fi x εi) και όχι με 30%. Το ποσοστό αυτό δηλαδή, είναι το σταθερό μέρος της εξίσωσης και όχι κάποιο σταθερό ποσοστό όπως το 30%