Αναζήτηση στην κοινότητα
Εμφάνιση αποτελεσμάτων για τις ετικέτες 'μαθηματικά'.
Found 3 results
-
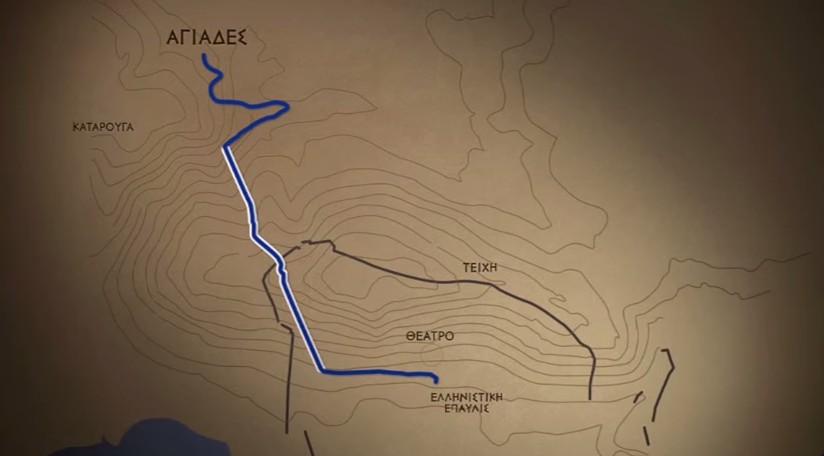
Το animation που ακολουθεί δημιούργησαν οι Θεοδόσης Τάσιος, ο Ν. Μήκας και ο Γ. Πολύζος της Εταιρείας Αρχαίας Ελληνικής Τεχνολογίας (ΕΜΑΕΤ). Ο Ευπαλίνος (6ος αιώνας π.Χ.) ήταν Μεγαρίτης αρχιτέκτονας. Το σπουδαιότεο έργο του ήταν το Ευπαλίνειον όρυγμα στη Σάμο, μια σήραγγα μήκους περίπου 1 χλμ. και διατομής περίπου 1,75 x 1,75 μ. Κατά μήκος της σήραγγας ο Ευπαλίνος κατασκεύασε έναν αγωγό, ο οποίος μετέφερε το νερό στην πόλη. Το έργο αυτό ένα από τα σπουδαιότερα τεχνικά έργα της αρχαιότητας, αν αναλογιστεί κανείς πως η κατασκευή του άρχισε συγχρόνως και από τα δύο άκρα του και οι σήραγγες που διανοίγονταν με αυτόν τον τρόπο, συναντήθηκαν στη μέση και αποτέλεσαν ενιαίο όρυγμα. Η πραγματοποίηση του έργου προϋπέθετε την ορθή επίλυση του σχετικού γεωμετρικού προβλήματος και την ακριβέστατη χάραξη πάνω στο έδαφος, με την επιπλέον χρήση των γνώσεων της Τοπογραφίας, της Γεωδαισίας και της Οπτικής που κατείχαν οι αρχαίοι Έλληνες από τον 6ο αιώνα π.Χ. Το έργο αυτό το ανέθεσε στον Ευπαλίνο ο τύραννος Πολυκράτης γιατί τον θεωρούσε έναν από τους σπουδαιότερους αρχιτέκτονες της εποχής του. Αυτό που το κάνει να ξεχωρίζει αιώνες μετά την κατασκευή του είναι το γεγονός ότι η σήραγγα ανοίχθηκε ταυτόχρονα και από τα 2 άκρα της. Η συνάντηση των σηράγγων έγινε κάτω από την κορυφή του βουνού με τεράστια μαθηματική ακρίβεια, παρότι οι γεωλογικές συνθήκες ανάγκασαν τον Ευπαλίνο να εκτραπεί πολλές φορές από την προσχεδιασμένη ευθυγράμμιση. Ενώ θα μπορούσαν να αποφύγουν την κατασκευή σήραγγας, και απλά να παρακάμψουν το βουνό και να υδροδοτήσουν την πόλη, σύμφωνα με τον ακαδημαϊκό Θεοδόση Τάσιο, ίσως ο μόνος πιθανός λόγος κατασκευής του Ευπαλίνειου ορύγματος, ήταν η επίδειξη της τεχνολογικής ικανότητας των κατοίκων της Σάμου. Δείτε το video animation: Δείτε όλες τις playlist από το Michanikos.gr webTV 1. 2. 3.
- 11 σχόλια
-
- τάσιος
- μαθηματικά
- (and 4 more)
-
Χαίρετε σύντεκνοι Έχω ένα πρόβλημα που με απασχολεί τον τελευταίο καιρό και δεν με αφήνει να κοιμηθώ τα βράδια... Έχω ένα τραπέζιο σχήμα με συγκεκριμένες διαστάσεις το οποίο δεν με ικανοποιεί ως προς το εμβαδόν του. θέλω να αλλάξω της διαστάσεις του ώστε να προκύπτει νέο ζητούμενο εμβαδόν. Οπότε το σκεπτικό μου είναι ως εξής... έστω αρχικό γνωστό τραπέζιο με ύψος Υα, βάση μικρή Β1α και βάση μεγάλη Β2α και εμβαδόν Εα. Θέλω το Εα να αυξηθεί και να γίνει Εβ οπότε προκύπτει νέο τραπέζιο με ύψος Υβ, βάση μικρή Β1β και βάση μεγάλη Β2β και εμβαδόν Εβ. Θέλω να αυξηθούν τα Υα , Β1α και Β2α ισόποσα (ή αναλογικά) ώστε να έχω εμβαδόν Εβ. π.χ. τραπέζιο με Υα = 1μ , Β1α = 2μ και Β2α = 3μ . Εμβαδόν Εα = 0,50 x 1 x (2 + 3) = 2.5τμ Θέλω να το Εα να γίνει Εβ = 3τμ... α) πόσο πρέπει να αυξηθούν ισόποσα τα Υα , Β1α , Β2α β) πόσο πρέπει να αυξηθούν αναλογικά τα Υα , Β1α , Β2α Με λίγα λόγια έχω τρία μήκη και θέλω να τα αυξήσω ώστε να προκύπτει το νέο εμβαδόν που θα ορίζω εγώ. Αν μιλήσουμε για excel θα με βόλευε να δίνω τα αρχικά τρία μήκη των πλευρών και το νέο ζητούμενο εμβαδόν και σαν αποτέλεσμα να παίρνω τρία νέα μήκη... ζητάω πολλά;
-
Το animation που ακολουθεί δημιούργησαν οι Θεοδόσης Τάσιος, ο Ν. Μήκας και ο Γ. Πολύζος της Εταιρείας Αρχαίας Ελληνικής Τεχνολογίας (ΕΜΑΕΤ). Ο Ευπαλίνος (6ος αιώνας π.Χ.) ήταν Μεγαρίτης αρχιτέκτονας. Το σπουδαιότεο έργο του ήταν το Ευπαλίνειον όρυγμα στη Σάμο, μια σήραγγα μήκους περίπου 1 χλμ. και διατομής περίπου 1,75 x 1,75 μ. Κατά μήκος της σήραγγας ο Ευπαλίνος κατασκεύασε έναν αγωγό, ο οποίος μετέφερε το νερό στην πόλη. Το έργο αυτό ένα από τα σπουδαιότερα τεχνικά έργα της αρχαιότητας, αν αναλογιστεί κανείς πως η κατασκευή του άρχισε συγχρόνως και από τα δύο άκρα του και οι σήραγγες που διανοίγονταν με αυτόν τον τρόπο, συναντήθηκαν στη μέση και αποτέλεσαν ενιαίο όρυγμα. Η πραγματοποίηση του έργου προϋπέθετε την ορθή επίλυση του σχετικού γεωμετρικού προβλήματος και την ακριβέστατη χάραξη πάνω στο έδαφος, με την επιπλέον χρήση των γνώσεων της Τοπογραφίας, της Γεωδαισίας και της Οπτικής που κατείχαν οι αρχαίοι Έλληνες από τον 6ο αιώνα π.Χ. Το έργο αυτό το ανέθεσε στον Ευπαλίνο ο τύραννος Πολυκράτης γιατί τον θεωρούσε έναν από τους σπουδαιότερους αρχιτέκτονες της εποχής του. Αυτό που το κάνει να ξεχωρίζει αιώνες μετά την κατασκευή του είναι το γεγονός ότι η σήραγγα ανοίχθηκε ταυτόχρονα και από τα 2 άκρα της. Η συνάντηση των σηράγγων έγινε κάτω από την κορυφή του βουνού με τεράστια μαθηματική ακρίβεια, παρότι οι γεωλογικές συνθήκες ανάγκασαν τον Ευπαλίνο να εκτραπεί πολλές φορές από την προσχεδιασμένη ευθυγράμμιση. Ενώ θα μπορούσαν να αποφύγουν την κατασκευή σήραγγας, και απλά να παρακάμψουν το βουνό και να υδροδοτήσουν την πόλη, σύμφωνα με τον ακαδημαϊκό Θεοδόση Τάσιο, ίσως ο μόνος πιθανός λόγος κατασκευής του Ευπαλίνειου ορύγματος, ήταν η επίδειξη της τεχνολογικής ικανότητας των κατοίκων της Σάμου. Δείτε το video animation: Δείτε όλες τις playlist από το Michanikos.gr webTV 1. 2. 3. Click here to view the είδηση
- 11 απαντήσεις
-
- 4
-

-
- τάσιος
- μαθηματικά
- (and 4 more)